www.zuse.de

Dokumentation des Baus der Z3

Horst Zuse

19. September 2014

Vorwort

Hier wird der Nachbau der Maschine Z3 für das Jahr 2010 dokumentiert. Es werden dazu aber keine Fotos veröffentlicht. Das erste Foto der gesamten Maschine Z3 wird erst am 26. Juni 2010 veröffentlicht werden, nämlich dann, wenn die feierliche Enthüllung der neuen Z3 im Konrad-Zuse-Museum in Hünfeld stattfinden wird.

Der Bau der Z3 orientiert sich an der Zeichnung rechts aus dem Jahr 1939 (Siehe Foto rechts).

Diese Dokumentation wird regelmäßig aktualisiert.

Weitere Arbeiten der der Z3 in 2011.

Dokumentation des Nachbaus

Bis 30. August 2009 - Abschluß der theoretischen Vorbereitungen

Alle Vorbereitungen theoretischer Art sind abgeschlossen.

7. September 2009 - Lieferung des Schrankes für das Rechenwerk

Der Schrank für das Rechenwerk ist in Auftrag gegeben und wird am  7. September 2009 geliefert.

Die Konsole wird im Dezember 2009 geliefert und die beiden Speicherschränke folgen im Januar 2010.

Ab 8. September 2009 -  Anlieferung der Relais

Um das Rechenwerk bauen zu können, sind 500 Koppelrelais mit 2 Umschaltkontakten und 150 Koppelrelais mit 4 Umschaltkontakten bestellt (Fa. FINDER) und geliefert worden. Dazu kommen Zeitrelais und die Stromversorgungen.  Weiterhin sind Kabelverbinder der Fa. WAGO bestellt, die es ermöglichen, die Speicherschränke und die Konsole anzusteuern.

12. September 2009 - Bestückung des Rechenwerkes Relais

Es werden die Register R1 und R2, sowie das Hilfsregister RH mit Relais für die Mantisse und den den Exponenten bestückt (Je 29 Relais).

13. September 2009 - Bestückung des Rechenwerkes (Mantisse)

Das Addierer der Z3 (Mantisse) wird mit 7 * 23 + 1 = 162 Relais bestückt. (Jedes Relais mit zwei Umschaltkontakten).

19. September 2009 - Realisierung der XOR und AND Schaltung

Die XOR und AND-Schaltungen für 22 Bit des Addierers (Mantisse) sind realisiert. Es folgt dann die Schaltung für den Übertrag.

20.September 2009 - Taktgeber

Der Taktgeber zum Schalten der Maschine ist realisiert. Gesteuert werden 10 Relais mit je 4 Umschaltern  im Takt von 1 Hertz zum Testen bzw. 5 Hertz im späteren Betrieb.  

23.September 2009 - 150 Verbinder

Von der Firma WAGO wurden heute 150 sogenannte Verbinder mit Schalter bestellt. Diese dienen zu zwei Zwecken:

1. Setzen der Bits in den Registern R1, R2 und RH (je 23 Bits). Dies dient zum Testen des Rechenwerkes.

2. Manuelles Setzen der Takte für das Rechenwerk und den Shifter.

Ab 30. September - XOR und AND

Realisierung der XOR und AND Schaltungen für den Binär-Addierer.  Zwei weitere Schaltungen müssen auch realisiert werden, nämlich XOR-N und AND-N, dies ist für die Subtraktion notwendig. Diese Schaltungen werden am 3. Und 4. Oktober realisiert. Diese Schaltungen werden in einem Takt erledigt.

Einige Anmerkungen zum Takt.  Der Taktgeber ist das „Herz“ eines Computers. Damit wird sichergestellt, das bei iner bestimmten Eingabe eine saubere definierte Ausgabe erreicht wird. Z.B. Wird die XOR und AND Berechnung in einem Takt durchgeführt, die Ergebnisse werden dann in einem zweiten Takt für den Übertrag verwendet. Damit ist sicher gestellt, daß unterschiedliche Reaktionszeiten der Relais keine Auswirkungen auf die Berechnung des Übertrages haben.

Danach wird der Übertrag realisiert, der in einem Schritt erfolgt.  Die oben erwähnten XOR *und AND* Schaltungen dienen zur Vorbereitung des einschrittigen Übertrages.

5. Oktober 2009 - XOR, XOR-N, AND, AND-N realisiert

Die XOR, XOR-N, AND, AND-N Schaltungen sind realisiert. Es warenca. 180 Kabel zu verschalten. Der ausführliche Test dieser Schaltung erfolgt am 6. Oktober 2009.

12. Oktober 2009 - Einschrittiger Übertrag

Der einschrittige Übertrag der Dualstellen ist realisiert.  Mit der nachfolgenden XOR-Schalung sind der Addierer und Subtrahierer fertig gestellt und werden ausführlich getestet.

17.-18. Oktober 2009 - Test des Addierers - Getaktete Relaiskette

Die Verdrahtungen für das Addierwerk und gleichzeitig für das Subtrahierwerk für die Mantisse sind fertiggestellt. Es folgen nun die ausführlichen Tests, ob das Rechenwerk wirklich nach Adam Ries rechnet. Danach wird das Addier- und Subtrahierwerk für den Exponenten realisiert, die Schaltungen sind fast identisch.

Getaktete Relaiskette

Wie ich oben schon ausführte ist das „Herz“ eines Computers der Takt. Alle Operationen in einem Computer werden Schritt für Schritt ausgeführt. Konrad Zuse nannte den Takt „Spiel“. Der Taktgeber in der neuen Z3 ist ein einstellbarer Zeitschalter, der dann mehrere Relais ansteuert. Die Taktfrequenz ist zum Testen 1 Hertz. Also, Klack, Klack ...., immer einmal pro Sekunde.

Um die z.B. die Addition durchzuführen, sind mindestens drei Takte notwendig, d.h. Es müssen drei logische Operationen sauber nacheinander ausgeführt werden. Es sind dies:

- XOR zwischen jedem Bit der beiden Operanden X und Y, also z.B. 5 und 7.

- AND zwischen jedem Bit der beiden Operanden X und Y, also z.B. 5 und 7.

- Der einschrittige Übertrag.

- Nochmals XOR, um das Ergebnis zu erhalten.

Um Besuchern genau demonstrieren zu können, wie die Z3 addiert, wird die Addition in 6 elementare Schriitte zerlegt:

- Jedes Bit des 1. Operanden (X) kann manuell gesetzt werden.

- Jedes Bit des 2. Operanden (Y) kann manuell gesetzt werden.

- Takt 1: Operand X wird in eine Relaiskette kopiert (X’).

- Takt 2: Operand Y wird in eine Relaiskette kopiert (Y’).

- Takt 3: XOR zwischen jedem Bit von X’ und Y’ wird berechnet und mit einer weiteren Relaiskette angezeigt (XOR).

Takt 4: AND zwischen jedem Bit von X’ und Y’ wird berechnet und mit einer weiteren Relaiskette angezeigt (AND).

- Takt 5: Der einschrittige Übertrag wird bestimmt.

- Takt 6: XOR zwischen XOR und AND wird bestimmt -> Ergebnis.

Um diese Takte, die bei der Konvertierung von Dezimalzahlen zu Dualzahlen und umgekehrt bis zu >40 Takten betragen können, realisieren zu können, ist eine Schaltapparatur notwendig. Konrad Zuse hat dies mit mechanischen Schrittschaltern durchgeführt (siehe oben). Für diese Schalter gibt es kein elektronisches Äquivalent.

Also, es muß eine Relaiskette her mit folgenden Eigenschaften:

Bei jedem Impuls durch den Taktgeber muß die Relaiskette von einem Relais zum nächsten schalten. Genau wie beim Schrittschalter muß solange Spannung am Ausgang anliegen, wie der Impuls durch den Taktgeber andauert.

Selbsthalterelais

Ein anderes Problem sind die Selbsthalterelais, die Konrad Zuse verwendet hat. Es sind Relais mit zwei Wicklungen, die heute kaum noch als moderne Relais erhältlich sind. Es ist also notwendig, die Selbsthalterelais durch moderne Relais mit einer Wicklung zu realisieren. Die beiden Wicklungen waren galvanisch total entkoppelt. Um dies zu mit modernen Relais mit nur einer Wicklung zu realisieren, werden von mir Dioden eingesetzt, die spottbillig sind (200 Stück, bis 75V, 150mA, ganze 2 Euro für 200 Stück).

Wie geht es weiter?

Nach den Test des Addierers und Subtrahierers wird der Shifter zum Ausgleich der Exponenten realisiert. Ich gehe von 10 Tagen aus.

Danach wird der Addierer/Subtrahierer für den Exponenten realisiert und getestet.

Dann folgt die Realisierung der Schaltungen für die Konvertierung der dezimalen Gleitkommazahlen in Binäre Gleitkommazahlen und deren Rückübersetzung.

Konsole der Z3

Die Struktur der Konsole der Z3 wird bereits geplant.  Es handelt sich dabei um die Ein- und Ausgabeeinheit  der Z3 im Dezimalsystem.

Ab 23. Oktober 2009 - Test des Addier- und Subtrahierwerkes

Der Test des Addier- und Subtrahierwerkes wird noch bis Anfang November  2009  andauern.

25. Oktober - 13.30 Uhr - Addierer und Subtrahierer funktionieren

Der Addierer und Subtrahierer (Mantisse) funktionieren.  Alle Tests zeigen korrekte Ergebnisse an. Mehr als 200 Relais sind verdrahtet incl. der beiden Operanden-Register R1 und R2. Ca. 1000 Schaltlitze (Kabel) wurden verlegt.

Nächster Schritt: Einbau der getakteten Relaiskette zur Steuerung des getakteten Addierers und Subtrahierers.

Von MO, 26.10. bis MI, 28.10  ist eine Pause angesetzt, da ich verreist bin.

Ab 31. Oktober 2009 - Test des Addierwerkes mit der getakteten Relaiskette

3. November 2009 - Getaktete Relaiskette und das  Addierwerk

Der Taktgeber zur Steuerung des Addier- und Subtrahierwerkes (Mantisse) ist fertig gestellt. Es ist eine modulare Einheit, bestehend aus 23 Relais, die auf einer Hutschiene montiert sind. Es kann damit der mechanische Schrittschalter simuliert werden.  Zur Ansteuerung sind 6 Eingänge notwendig, 10 Ausgänge steuern den Takt.

Mit dieser Relaiskette wird am 4. November der automatische Ablauf der Addition bzw. Subtraktion der Mantisse getestet.

4. November 2009 - Getaktetes Addier- und Subtrahierwerk  voll funktionstüchtig

Seit genau 18.20 Uhr am heutigen Tag funktioniert das Addier- und Subtrahierwerk (Mantisse) einwandfrei, und zwar durch den Taktgeber und die getaktete Relaiskette gesteuert.

8. November 2009 - Addierwerk des Exponenten im Test

Seit heute wird das Addier- und Subtrahierwerk des Exponenten getestet.  Dies ist eine Voraussetzung dafür, daß z.B. zwei Gleitkommazahlen gemäß der Potenzrechnung korrekt addiert werden können.  Wie addiert man zwei Potenzen? Angleichung der Exponenten und dann die Mantisse addieren.

12. November 2009 - Test des Exponenten-Addierers und Subtrahiers abgeschlossen

Das Exponenten-Addierer- und Subtrahierwerk laufen einwandfrei.

Ab 13. November 2009 - Große Weiche - Shifter für die Mantisse

Um Gleitkommazahlen addieren zu können, müssen vor der Addition die Exponenten ausgeglichen werden. Dazu wird die Zahl mit dem kleineren Exponenten an den der größeren Zahl angepaßt und die Mantisse wird entsprechend viele Stellen nach rechts verschoben.

Der Shifter kann aber die Mantisse auch bis zu 15 Stellen nach links verschieben, dies wird zur Normalisierung der Gleitkommazahl bei der Subtraktion benötigt.

17. November 2009 - Große Weiche arbeitet korrekt

Viele Kabel (Schaltlitze) waren für die Verdrahtung der  Großen Weiche notwendig.

Vom 18.11.-22.11.2009 Pause - Dienstreise - Urlaub

Ab 23.11.2009 - Test des Shifters (Große Weiche)  zusammen mit dem Exponenten-Addierer bzw. Subtrahierer.

Der Test des Shifters hat begonnen, dabei sind viele Dinge zu beachten.  

Dann folgt der Test des Shifters zusammen mit dem Exponentenrechenwerk, welches die Differenz der Exponenten berechnet. Danach wird die Taktsteuerung modifiziert.

30.11.2009 - Shifter für die Mantisse (Große Weiche)  arbeitet einwandfrei

Jetzt arbeitet der Shifter für die Mantisse einwandfrei.  Es gab einige Probleme, da ich bei den Hunderten von Schaltlitzen zwei vertauscht hatte. Nur eine genaue Durchmessung mit einem Voltmeter, übrigens Baujahr 1958, half mir, diesen Fehler zu finden.  Dazu kam, daß ein Relais fehlte.

Der Shifter wird durch fünf Relaisketten gesteuert, insgesamt 88 Relais. Es sind 32 Shiftkombinationen möglich. Um diese Kombinationen zu testen, wird das Exponentenaddierwerk erweitert, welches dann von 0-31 wie ein Binärzähler zählt. So kann ich die 32 Positionen des Shifters demonstrieren.

9. Dezember - Beide Addierwerke arbeiten einwandfrei

Die Exponenten- und Mantissenaddierwerke arbeiten einwandfrei.

 

10. Dezember 2009 -  Addition nach der Potenzrechnung

Die Addition und Subtraktion in der Z3 folgt der Potenzrechnung, wie man diese in der Schule lernt.

Also, zwei Zahlen, dargestellt als Potenzen, werden addiert, indem man die Exponenten angleichen muß (11. Klasse). Das ist nun dran. Dazu brauche ich das Addier- Subtrahierwerk des Exponenten.  Das sind etwas komplizierte Schaltungen.

Es folgen dann spannende Schaltungen zur Ausrichtung der Mantisse, d.h. der Normalisierung der Mantisse nach der Addition und der Subtraktion. Hier gibt es ein Problem. In der Beschreibung von Konrad Zuse, aber auch in dem Buch von Raul Rojas: Die Rechenmaschinen von Konrad Zuse, welches eine Darstellung des Patentes Z391 von 1941 ist, also eine aufbereitete Darstellung dieser Patentanmeldung, gibt es Widersprüche.

11.  Dezember 2009 -  Konvertierung der  Dezimalzahlen in Dualzahlen und umgekehrt.

Parallell bereite ich schon die Konvertierung der Dezimalzahlen bei der Eingabe in Dualzahlen vor. Ab Februar 2010 wird dazu diese Konsole bereit stehen, die hier in Berlin nochmals angefertigt wird (siehe rechts).  Testen werde ich dies allerdings jetzt ganz primitiv mit dezimalen Drucktastern.

16. Dezember 2009 - BCD-Code

Die Eingabe auf der Konsole erfolgt Dezimal, und zwar mit Mantisse und Exponent, ebenso die Ausgabe.

Getestet wird die dezimale Eingabe mit einer einfachen Dezimaltastatur. Zu jeder Dezimalziffer wird die Dualzahl bestimmt und dann wird es spannend:. Die vier eingegebenen Dezimalzahlen der Mantisse müssen in das Dualzahlensystem übersetzt werden. Dies geschieht mit dem Addierwerk der Mantisse in acht Takten.

Weihnachen - Silvester - Es wird weiter gebaut

Es folgt dann die Konvertierung der Dualzahlen in das dezimal Gleitkommsystem. Eine anspruchsvolle Schaltung, aber ....warten wir es ab.

26. Dezember 2009 - Kleine Weiche

Während die große Weiche dazu dient, die Mantisse 16 Bit nach rechts oder 15 Bit nach links zu schiften, kann die Kleine Weiche ein Bit nach links und zwei Bit nach rechts schiften.

Die kleine Weiche besteht aus 36 Relais mit einem Umschalter. Sie wird für die Konvertierung von Dezimalzahlen in Dualzahlen benötigt, aber auch für die Multiplikation.

Notation des Zyklus - 27. Dezember 2009

Konrad Zuse schreibt, aber auch in dem Buch von Raul Rojas (Hrsg.): Die Rechenmaschinen von Konrad Zuse, 1998, wird angegeben, daß die Addition in 3 Zyklen durchgeführt wird. Okay, 3 Zyklen.  

Aber bei der Konvertierung  von vier eingegeben Dualzahlen mit vier Dezimalstellen in eine Mantisse wird ausgeführt, daß dies 9 Zyklen dauert. Es sind dabei aber  8 Additionen durchzuführen! Es müßten also 8x3 = 24 Zyklen sein.   

Der Trick ist folgender: Die drei Zyklen für die Addition werden in einem Zyklus der Konvertierung versteckt und während dieses Zyklus auch abgearbeitet. Es müßte 3 Schritte/Spiele heißen, die innerhalb eines Zyklus ablaufen.

Es ist hier eine ungenaue Notation.

Ich bezeichne die Operationen, die innerhalb eines Zyklus ablaufen, als Elementaroperationen.

27. Dezember 2009 - Didaktik

Enorm wichtig ist bei dem neuen Nachbau Z3, daß die Grundstrukturen eines Computers / Rechners didaktisch gut präsentiert werden können.

Dazu ist die neue Z3 so konzipiert, daß alle Komponenten separat als Elementaroperationen demonstriert werden können, wie z.B:

• Die Eingabe einer Dezimalzahl und deren Umwandlung in eine duale Gleitkommazahl
• Die Kopie des Inhaltes eines Registers in ein anderes Register.
• Demonstration der großen Weiche, welche 15 Bits nach links oder 16 Bits nach rechts shiften kann.
• Umwandlung einer dualen Gleitkommazahl in eine dezimale Gleitkommazahl.
• Die Addition und Subtraktion Schritt für Schritt.

Ab 29.12.2009 - Realisierung aller Elementaroperationen

Es werden jetzt alle Elementaroperationen realisiert. Dies wird ca. 2-3 Wochen dauern. Danach werden diese Elementaroperation in Zyklen zusammen gefügt und ganze Rechnungen können mit der Z3 durchgeführt werden.

Ziel ist, das Rechenwerk bis Ende Januar 2010 funktionsfähig zu haben.

Architektur der Z3 siehe hier.

6. Januar 2010 - Lieferung des Speicherschrankes I

Der erste Speicherschrank ist geliefert worden. Die Bestückung mit ca. 800 Relais beginnt in der Woche vom 18. Januar 2010.

12. Januar 2010 - Tests

Ab heute beginnen die Tests für die Addierwerke der Exponenten und der Mantisse mit allen Shiftern und Schaltern (Siehe die Zeichnung der Z3).

Für die Konvertierung einer dezimalen Gleitkommazahl in eine Binäre werden fast alle Komponenten der Z3 benötigt, daher ist dies ein idealer Testfall.

23. Januar 2010 - Normalisierung der Mantisse realisiert

Das ist eine interessante Schaltung. Es geht darum, die Mantisse in eine normaliesierte Form zu bringen, also:

0.000010101 nach 1.0101.

Dazu muß bestimmt werden, um wieviel Stellen die Mantisse nach links verschoben werden muß. Das wird dann mit der großen Weiche gemacht.

31. Januar 2010 - Test der Normalisierung der Mantisse

Der Test der Normalisierung der Mantisse ist erfolgreich, die Verdrahtung stimmt.

Es sind nun alle Elementarkomponenten der Z3 realisiert.  Was bedeutet dies? Die Architektur der Z3 ist hier dargestellt.  Sehr aufwendig ist die Realisierung der „Schalter“ Fc, Fa, Ff, Fb, Fd, und letztlich der Multiplexer von Be nach Be1.

Danach werden die beiden Speicherschränke verdrahtet.  

6. Februar 2010 - Umfangreiche Tests des Rechenwerkes

Bis heute Abend hoffe ich, die Leitungen für die Datenbusse  realisiert zu haben.

Es beginnen nun die Tests des Zusammenspiels der Komponenten der Z3. Konrad Zuse hat dies mit Schrittschaltern realisiert. Es handelt sich um folgende Operationen:

• Addition
• Subtraktion
• Multipliplikation
• Division
• Quadratwurzel
• Eingabe einer Dezimalzahl
• Ausgabe einer Dezimalzahl

Ich realisiere dies mit Zeitschaltern der Fa. FINDER.

8. Februar 2010 - Datenbusse

Die Datenbusse sind nun realisiert. Dies war eine sehr aufwändige Verdrahtung.

Es sind immer 18 Leitungen bzw. 8 Leitungen zu schalten.

Die Schalter sind gemäß Zeichung der Z3: EC, Eg, Ea, Ee, Eb, Eh, Ei, Ed, Fc, Fa, Fb, Fd, Ff, Be’1.

Jeder dieser Schalter kann per Hand geschaltet werden, das sind die Elementaroperationen.  Dazu kommen die Elementaroperationen für die Addition, usw. Die Abläufe der Elementaroperationen werden dann durch den Zyklus gesteuert.

8. März 2010 - Wie die Zeit vergeht  

Ich habe tatsächlich vergessen, den Nachbau der neuen Z3 seit dem 8. Februar 2010 zu dokumentieren. Es lag wohl am täglichen Verkabeln der Komponenten der Z3.

Es ist viel passiert:

Alle Elementaroprationen sind funktionsfähig, d.h.:

Alle Register sind als Halterelais geschaltet.

Alle Datenbusse sind geschaltet.

Normalisierung der Mantisse funktioniert.

Differenz der Exponenten und die Auswirkungen auf die Mantisse sind geschaltet.

Dezimal-Binärkonvertierung ist geschaltet.

Was kommt nun:

Das Zusammenspiel aller Komponenten für die Addition, Subtraktion, Dezimal<->Binär Konvertierungen usw. Das wird bis Ende März 2010 dauern.

Parallel werden die beiden Speicherschränke verdrahtet.

Im April wird die Konsole verdrahtet. Da gibt es ein Geheimnis. Mehr dazu später.

22.5.2010: Umfangreiche Tests

Es gibt beim testen immer wieder Überraschungen, Fehler, die manchmal mehrere Stunden zeit kosten. Die Ursachen sind Unachtsamkeit, bei der Verdrahtung, aber auch einfach logische fehler in den Schaltungen.

Denn, der neue Nachbau der Z3 unterscheidet sich von den anderen beiden Nachbauten deutlich, denn:

Jede Komponente kann einzeln demonstriert werden.

Getestet sind nun:

Die Normalisierung der Mantisse.

Die Differenzenbildung des Exponenten für die Potenzrechnung, d.h.: 5-3 ist nicht gleich 3 -5. Dazu müssen die beiden Shifter entsprechen geschaltet werden.

Das Addierwerk.

Die Shifter.

Die Konvertierung von Dezimalzahlen in Binärzahlen.

Die Addition von positiven Zahlen.

September 2010

Noch zu realisieren sind:

Die Binär<->Dezimalkonvertierung, ein wirklich komplizierter Algorithmus.

Siehe auch die PDF.

25. Januar 2014

Rückübersetzung

Rückübersetzung Binär-> Dezimal läuft einwwndfrei.

Dies ist ein sehr komplizierter Algorithmus, der durch eine SPM und einen Schrittschalter realisiert wird.

Speicherwerke

Die beiden Speicherwerke sind angeschlossen.

Nächste Aktivität

Nächster Punkt: Gleitkommaarithmetik.

Ab Juni 2014

Gleitkommaarithmetik

Horst Zuse

 

Zeichnung der Original-Z3 aus dem Jahr 1939.

Schrittschalter. Mit diesen Baustein wurden in der Original-Z3 von 1941 die Mikrosequenzen der Z3 gesteuert, wie z.B. die Multiplikation oder die Umwandlung von dezimalen in binäre Gleitkommazahlen.

Im Nachbau 2010 wird dieser Schrittschalter durch eine getaktete Relaiskette realisiert. Da z.B. Die Umwandlung von dezimalen Gleitkommazahlen in binäre Gleitkommazahlen 41 Takte benötigt, ist eine Relaiskette bestehend aus 80 Relais notwendig.

Es ist schon erstaunlich, wie aufwendig die Realisierung des obigen Schrittschalters durch eine getaktete Relaiskette ist.

Koppelrelais mit zwei Umschaltkontakten und einer Leuchtdiode der Fa. FINDER. Im Rechenwerk werden davon ca. 500 Stück installiert.

Ein- und Ausgabeeinheit der Z3.

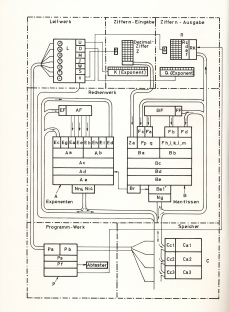
Gesamtarchitektur der Z3, gezeichnet von Konrad Zuse.